Introduction

Most Target customers have probably had experience with the slow self-checkout mess and the chronically long lines. They seem to have planned for much better throughput than they actually get and cashier staffing is not sufficient for demand in reality. This is a labor model problem and in this post we'll look at labor models in contact centers and retail stores, and where things might've broken down at Target.

So what is a labor model? Labor models are a tool to estimate labor requirements give a body of work to be performed. They're used for budgeting, staffing planning, and scheduling. Specific implementations vary based on the work being done and the quality of data available about that work. This post will cover labor model basics, the major types, and labor model examples from contact centers and retail stores.

Background

I ended up in workforce management (WFM) accidentally after about a year as a contact center agent answering product information questions about boat parts. One of my first projects was getting our unmaintained, end-of-life WFM platform (TotalView IEX) generating forecasts and schedules again (the team had reverted to copying the same schedules forward each week after the departure of the previous WFM manager more than a year prior).

This was my first meaningful exposure to labor models but I'd eventually end up building my own models in Excel, SQL, and Python for both contact centers and retail stores.

What is a labor model?

Let's look at a problem statement: you have some body of work and you need to determine how much labor is needed to complete it. For example, you have a contact center that takes phone calls and you need to know how many agents you need to answer the phone.

In the generic case, we can think of doing any given body of work as producing widgets. Widgets in practice could be stuffing envelopes, answering phone calls, or stocking shelves, but they're all some unit of work. The labor model is what gets us from units of work to labor hours. In the simplest model, this is work units multiplied by average time per unit produced:

\[ \textit{Units of work} \times \textit{Seconds per unit of work} = \textit{Labor hours}\]

We can also call the unit of work demand or volume and time per unit of work a labor standard or handle time.

Why do we need labor models?

Broadly, for many kinds of planning purposes. Specifically, for things like budgetting, staffing and hiring plans, and scheduling.

Budgetting, so finance can estimate and allocate payroll. Staffing planning, to determine how many people you need to hire and when. Scheduling, to estimate how many people you need to have working at any given time. Additionally, things like real-time monitoring and performance retrospectives also benefit from input from labor models.

The specific use-case will influence the level of detail and accuracy required from a model. For example, a budgeting model might only need to give us output by month, while a scheduling model goes to 30- or 15-minute intervals.

Where labor models fit in the bigger picture

Labor models are one piece of a workforce management process. The volume and handle time inputs often come from a forecast model that predicts future volume and labor model outputs will be used to drive staffing and budget models.

In the best case your time series data comes from a robust time series forecast model that can predict volume at a high level of granularity (e.g., down to 30-minute intervals). But often it's actually copy/pasting a previous period, doing simple exponential smoothing on recent historical data, or simply made up. Accurate forecast data is one of the most critical pieces of a labor model.¹

A separate staffing model assists with planning onboarding capacity and employee attrition. For example, if you know you'll need an extra 50 agents by the peak of demand in July, but you can only onboard 5 agents per week, the staffing model will calendar out hiring.

A budget model takes either labor hours or headcount to calculate payroll (and other employment) costs for finance. These models may layer in overhead roles like managers, trainers, and quality assurance and additional costs like benefits, taxes, and bonuses. Often these models are controlled by finance and the WFM team will simply provide the labor hours or headcount numbers.

Types of labor models

There are two primary ways to approach structuring a labor model: bottom-up and top-down.

Top-down

A top-down model takes a high-level view of some summary value for a given body of work and calculates the labor requirements off that single value. An example for retail stores is taking sales $ and working backwards to transactions through the register to estimate labor hours. E.g.,

1. Start with total sales.
2. Divide sales by average transaction value to get a transaction count.
3. Apply a transactions per labor hour ratio to get labor hours.

The specific transactions per labor hour ratio may be based on a given store's type, determined by sales volume and often modified by square footage or some other sizing factor and will usually scale non-linearly with sales volume.

Note the labor ratio gives a labor hours result that includes all of the work that goes into running a store, not just checking out customers. This is what makes the model top-down.

This is a good approach when you only have high-level data available (or the quality of your low-level data is poor) and, assuming your algorithm is good, you will generally get workable labor requirements at least at the aggregate levels (weekly or monthly).

Where it can break down is when you start layering in post-calculation modifiers like number of entrances, stores in high-crime areas, specialty departments, etc. These can be difficult to account for in a top-down model, can lead to staffing variances to actual requirements, and make the model harder to maintain. Explainability is also more difficult when you're overloading a modifier field with a lot of different factors.

I'm not diving into the forecasting portion of labor models here, but because top-down models are built on one high-level metric, forecasts tend to be easier to build. An overall sales number is minimally noisy and has high data quality compared to individual work items.

Bottom-up

If a top-down model expands downward from a high-level number, a bottom-up model takes a low-level view of the work where you count as many work inputs as possible (e.g., transactions, price changes, receiving, restocking, cleaning, etc.) and calculate labor hours by adding the totals up for all of the individual work items. This is calculated by adding "handle time" (contact centers) or "labor standards" (retail stores), which is how long (on average) it takes to complete a work item. For example, say the average time it takes to change a price tag on a shelf is 20 seconds. If you have 100 price changes to do, to calculate the labor requirement:

\[ \textit{Work inputs} \times \textit{Handle time} = \textit{Labor hours}\]

\[ 100 \textit{ price changes} \times 25 \textit{ seconds} = 2500 \textit{ seconds}\]

or 33.3 minutes, of labor required to complete 100 price changes.

If you combine several of these workload calculations for different work items, you get a total labor requirement for the store.

Work input	Demand	Labor standard	Labor hours
Price changes	100	25 seconds	0.7 hours
Truck receiving	3	2 hours	6 hours
Restocking	100	3 minutes	5 hours
Cleaning	5	1 hour	5 hours
Transactions	400	3 minutes	20 hours
Promo signs	120	1 minute	2 hours
Total			38.7 hours

Bottom-up is better when you have good data available for a lot of your major work items. Explaining the labor requirement is straightforward: "We have X work inputs and each one takes, on average, Y minutes to complete." It's also easier to layer in post-calculation modifiers because you can simply add them as an additional work item and still see what's driving the labor requirements (like a flat 40 hours per week for stores with an upstairs second entrance).

Bottom-up doesn't work without data or with poor quality data. It can also be difficult to get a good handle time or labor standard for each work input as most of them won't be systematically tracked and performing time studies is expensive and often flawed. There's also more data flowing through the model than with a top-down model, so it can be harder to manage at scale. The data gathering and validation phase was the most time consuming part of one large-scale retail labor model I worked on (though bad processes and lack of automation drove a lot of the overhead).

Work types

Work inputs fall in two categories: workload (low time-preference) and service level (high time-preference). This is the primary difference between contact center and retail store models. Put differently, people waiting in a phone queue care about how long it takes you to answer the phone, but restocking shelves or updating price tags doesn't have the same kind of urgency (time preference).

Workload

For the bottom-up model we talked about labor hours coming from multiplying work inputs by handle time or labor standards. This gives you workload, but assumes that you have infinite capacity to handle that workload and widgets flow through one after the other. This is a good assumption for things like stocking shelves, cleaning, or doing price changes, as there is generally a lot of flexibility in when that work can be done. When your model includes a lot of workload tasks and relatively few service level tasks (e.g., register transactions) you can treat the whole bundle as workload based and let the service level tasks be absorbed by the workforce as they come in (e.g., call people stocking shelves up to open a register when there's a long line).

Service level

For service level work, we take the workload approach but layer in a service level requirement. In a contact center, something like Average Speed of Answer (ASA) or Service Level (SL). This takes the formula from simple units * time to something that integrates a service level calculation. This is often Erlang C (more below) or simulation models.

Compared to retail, contact center agents are doing almost exclusively service level work, so there isn't slack in other workload tasks to absorb variations in service level tasks.

There's an objection here that waiting in line to check out is undesireable and it's clearly a service-level task with high time preference. This is true, but there's nothing to collect data on queue wait times for individual transactions² so there's no data to calculate service level with. Plus, unlike a contact center where agents are more specialized and focused, you can shift workers around to accomodate bumps in demand to keep wait times under control (e.g., have people stocking shelves come up to the registers).

Erlang C

Briefly, Erlang C can be used to calculate the number of agents required to hit a specific service level if the interval length, number of contacts, average handle time, and service level target are known. The formula is:

\[ P_W = \frac{\frac{A^N}{N!}\frac{N}{N-A}}{(\sum_{i=0}^{N-1}\frac{A^i}{i!}) + \frac{A^N}{N!}\frac{N}{N-A}}\]

Where \(P_W\) is the probability of waiting, \(A\) is the traffic intensity in Erlangs (call hours), and \(N\) is the number of agents. See this explanation of Erlang C for more.

Model types

Between service level/workload and top-down/bottom-up this gives us three types of labor models:

• Workload (top-down)
• Workload (bottom-up)
• Service level (bottom-up)

The fourth obvious combination, a top-down service level model, doesn't work because you can't do service level calculations without handle time and detailed counts of work inputs.

Any given labor model may mix elements of these types. For example, a contact center might have service level calculations for calls and chats, but treat emails as workload. Mixing top-down and bottom-up is less common, but you might have a top-down model for most of the work and a bottom-up model for a few key work items.

Examples

Contact center example

Let's say we have a contact center with 100 agents that experiences significant increases in volume during the summer. The center handles a mix of phone calls, emails, and chats. We want to determine how many agents we need staffed to maintain consistent service levels for every channel to plan for hiring going into summer.

Since contact centers memorialize every interaction, we have both contact volume and handle time information available for every interaction. With this data detail, we could model labor requirements in as much or as little detail as desired.

The mix of calls, chats, and emails will usually be treated as two service-level work items (calls and chats) with email as a workload item. Even with a 4-hour target response time for emails, the time-preference is low enough that we can treat it as workload.

For email we have handle time data and volume data, so we just multiple the two to get labor hours. For calls and chats, we can use Erlang C to calculate the number of agents required to hit a specific service level target. We can then sum up the labor requirements for each channel to get the total labor requirement for the contact center.

In practice, a lot of WFM tools will take into account routing behaviors and overlap between channels to calculate more accurate labor requirements. For example, if you have agents who can handle both chats and emails, you can staff fewer agents than if you had separate pools of agents for each channel, especially as the overstaffing you'd normal plan for to handle variations in arrival patterns for chat can be absorbed by having the higher-time-preference chat contacts take priority over the lower-time-preference emails.

Top-down retail store example

A different example: you have a couple hundred retail stores ranging in size from one or two employees to a couple dozen. You need to plan out payroll allocation by week for each of these stores for the next year. Employees in these stores are responsible for check out, stocking shelves, updating price labels, cleaning, product assistance, and other tasks. You only have sales data available.

With only sales data, all labor calculations have to flow from sales:

1. Start with sales $ by week for each store.
2. Calculate an average order value for each store type.
3. Determine the store type or size based on something like total annual sales or store square footage.
4. Calculate transactions by dividing sales by average order value for that store type.
5. Calculate labor hours per transaction ratio based on sales volume band.
6. Calculate labor hours by multiplying transactions by labor hours per transaction ratio.
7. Layer in labor hours from any post-calculation modifiers (e.g., stores with a second entrance, specialty departments, etc.).

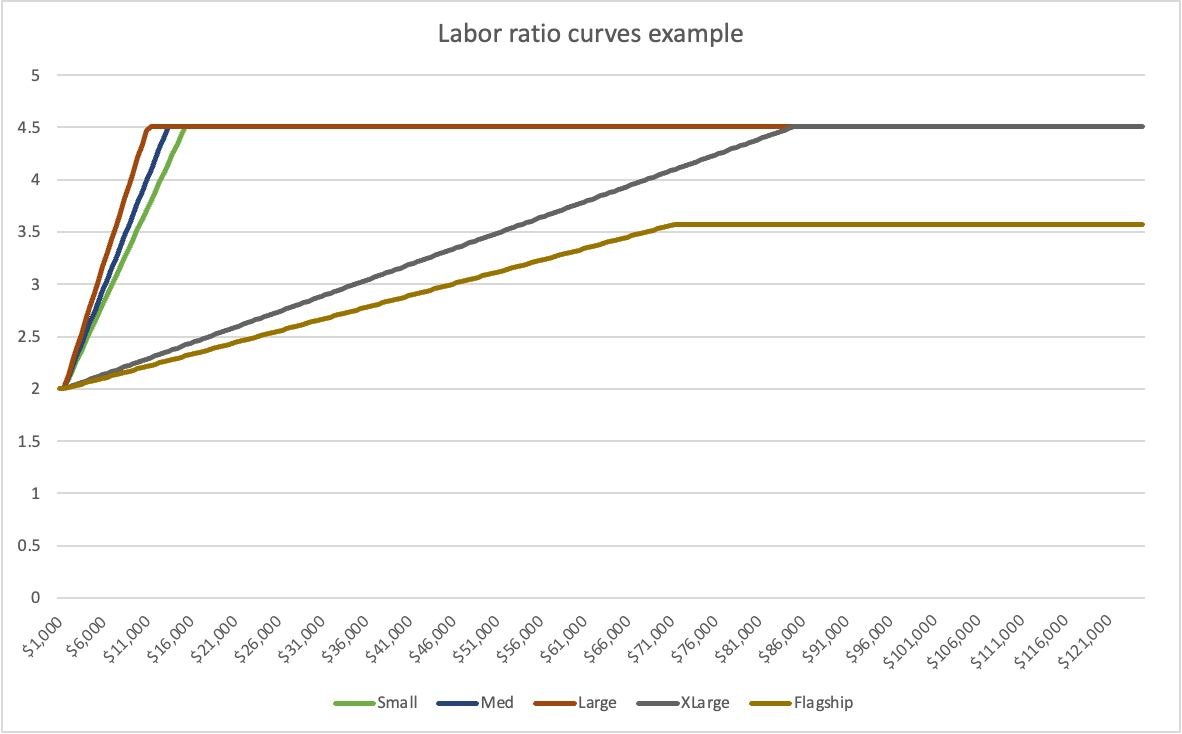
In step 3, different store types will generally have slightly different labor hours per transaction ratio curves. This should be to capture differences in efficiency and labor requirements at different store sizes, but often mostly amounts to "cost control" or putting the most money into the most profitable stores in practice.

In step 5, the sales volume band will generally decrease the labor hours ratio so you get fewer labor hours per transaction as sales increase to account for increased efficiency at higher sales volumes.

Determining labor hours per transaction ratios

The hours-per-transaction ratio number elides a lot of complexity since it's attempting to capture a complete picture of almost all of the labor going into running the store from a single number. This requires extrapolating out all of the tasks to run a store that are behind a single transaction. Generally this number will need to be arrived at through a close familiarity with the business and store operations plus experimentation.

Bottom-up retail store example

Let's take our last example but say we have detailed, accurate data for most of the major labor drivers within the store. We know how many transactions and of what types are going through the registers, how many price change stickers get printed per week, the weekly volume of replenishment shipments, specialty department sales (e.g., photo printing), inventory counts, etc. We also have data on how long each of these tasks takes on average thanks to the efforts of industrial engineers and their time studies.

With this data, we can build a bottom-up workload model that calculates labor hours for every significant work item we have data for:

1. Start with a count (demand) and a labor standard for each work item.
2. Multiple the count by the labor standard to get labor hours for each work item.
3. Sum up all the labor hours to get total labor requirement for each store.
4. Layer in any additional labor requirements (e.g., second entrance, specialty departments, etc.).
5. Add in any post-calculation modifiers (e.g., a floor for business operating hours, labor hours cap, cap on year-over-year labor hours change, etc.).

With each intermediate step we can examine the labor requirements and constraints are explainable and modifying any part of the model is straightforward.